赛后大体总结:
$GDOI$ 第一天的感悟还是挺多的,从中也学到了很多东西(虽然成绩不咋样)
也希望明天的考试继续加油
解题报告
T1 邹忌讽齐王纳谏
题意
有 $n$ 个建议记录,按时间顺序罗列
每条建议形如“$name \ way$”,其中 $name$ 是由小写英文字母组成的字符串表示提建议者的名字;$way$ 是一个为 $1$ 、$2$ 或 $3$ 的数字,表示提建议的方式
建议方式为 $1$ ,则获得价值为 $A$ 的奖励
建议方式为 $2$ ,则获得价值为 $B$ 的奖励
建议方式为 $3$ ,则获得价值为 $C$ 的奖励
输出这些人之中获得奖励总和最多的是谁,他总共获得了多少奖励。如果获得最多奖励的不止一个人,请输出最早获得最多奖励的人
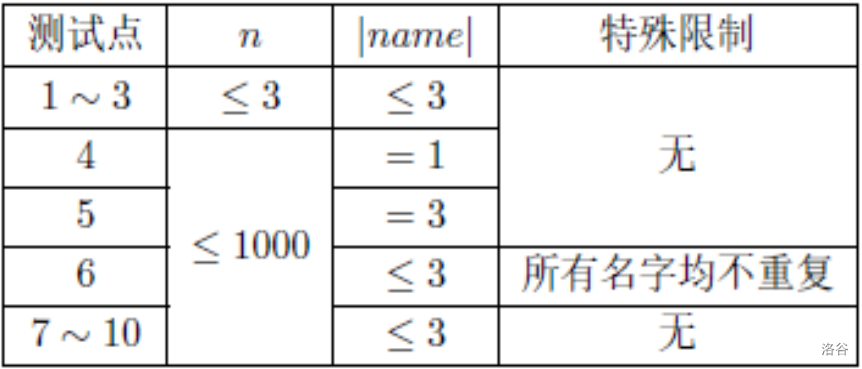
数据范围
对于所有测试点,$0 \leq A,B,C \leq 1000$ ,$1 \leq n \leq 1000$ ,$1 \leq |name| \leq 3$
思路
很明显一道签到题小模拟
法一: $100\ pts$
暴力枚举,扫描出现的名字
时间复杂度 $O(n^2)$
法二: $100\ pts$
由于 $|name| \leq 3$
$\therefore$ 可以将 $name$ 视为一个 $26$ 进制数,范围在 $1$ 到 $26+26^2+26^3$ 之间
时间复杂度 $O(n)$
这两种方法都能 $AC$ 这道题
T2 数列游戏
题意
有一个长度为 $n$ 的序列 $a_1$, · · · , $a_n$ 。
如果序列的长度大于 $1$ ,那么你就能进行操作,每次操作可以选择两个相邻的数 $a_i$ , $a_{i+1}$ 合并,得到一个新的数 $a_i \oplus a_{i+1}$,每次操作都会使序列的长度减少1。
你需要进行若干次操作(可能是 $0$ 次),使得最终序列任意子区间的异或和不为 $0$ 。子区间的定义为连续的一段数 $[a_l, a_{l+1}, · · · , a_r]$ ( $l \leq r$ )。求满足条件的最终序列的最长长度。
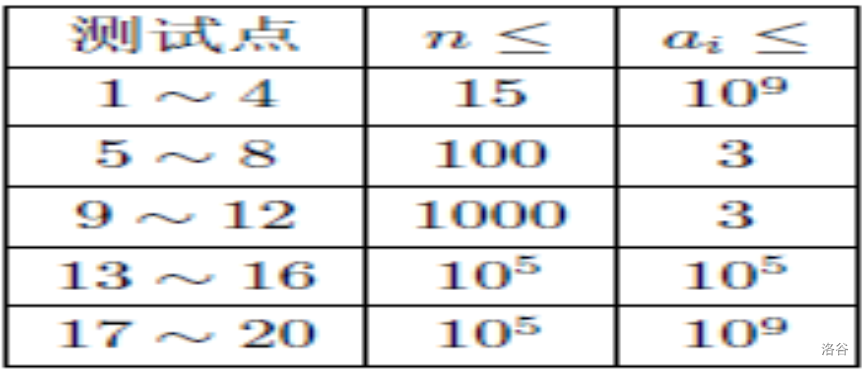
数据范围
对于所有测试点,$1 \leq n \leq 10^5$ ,$0 \leq a_i \leq 10^9$
思路
法一: $0\ pts$
模拟异或,验证当前序列是否满足题意
时间复杂度 $O(n!)$
法二: $20\ pts$
可以发现,每次合并会将序列变成若干个段,举序列 $4\ 5\ 6\ 7$ 为例
若要合并 $4\ 5\ 6$ ,则序列就会变成 $(456)\ 7$
但在题意中 $4\ 5\ 6$ 合并的顺序其实对结果没有影响
所以可以枚举各段的分界线
时间复杂度 $O(2^n)$
法三: $40\ pts$
$\because a_i \leq 3$
$\therefore$ 无论怎么异或,得到的结果一定 $\leq 3$
$\therefore$ 最终序列长度不会超过 $3$
$\therefore$ 只有 $2$ 条分界线
那么就可以使用前缀异或和
设 $S_i=a_1 \oplus a_2 · · · \oplus a_i$
则 $a_l,· · ·,a_r$ 的异或和就是 $S_r \oplus S_{l-1}$
法四: $100\ pts$
设最后分段为:
则每一段的异或和为 $S_{v_i} \oplus S_{v_{i-1}}$ ,第 $l$ 段到第 $n$ 段的异或和为 $S_{v_r} \oplus S_{v_l}$
题目要让最后任意非空子区间异或和不为 $0$ ,也就是说任意 $S_{v_i}$ 不相同且不为 $0$
$\therefore$ 要让最后的序列长度最长,就要从 $S_1,· · ·,S_n$ 中选最多的不相同且不为 $0$ 的数字
统计 $S_1,· · ·,S_n$ 中出现过多少种不同且非 $0$ 的数字即可
T3 流水线
题意:
流水线就是将 $CPU$ 分成若干个任务模块,而一个模块又可以继续划分成更小的模块,小模块可以划分成更小的小小模块
把一个任务划分后,每一个部分的代价会变少,但是可能会产生额外的代价
我们可以用一棵以 $1$ 为根的有根树来描述模块之间的关系,每个节点是一个模块,每个节点的点权对应着该模块的时间代价。每一个非叶子节点可以划分成该节点的儿子节点对应的模块。
每个模块都有一定的时间代价,而流水线最后的效率我们可以用划分的模块数乘上模块中时间代价最大的一个来表示,时间代价越小,流水线的效率越高。也就是说,假如小明最后把 $CPU$ 划分为了 $m$ 个模块,每个模块的代价为$w_1,w_2, · · · ,w_m$ ,则总代价为$m \times \max(w_1,w_2, · · · ,w_m)$。
另外,我们认为根节点对应的模块不往下划分模块也是一种合法的方案。
最后效率最高的流水线设计方案
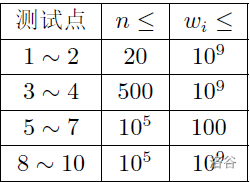
数据范围:
对于所有测试点,$1 \leq n \leq 10^5 , 0 \leq w_i \leq 10^9 , w_i \leq w_{f_i}$
思路
法一: $25\ pts$
枚举每个点选择拆分或者不拆分
时间复杂度 $O(2^n)$
法二: $50\ pts$
对于每个 $m$ ,可以求出最小的 $\max(w_1, · · · ,w_m)$
用树形 $DP$ 的思想解决
设 $f[i][j]$ 表示以 $i$ 为根的子树,且选择了 $j$ 个点,根是否选择,能达到最小的 $\max(w_1, · · · ,w_m)$
转移:
- 选择 $i$ 节点
- 不选择 $i$ 节点
时间复杂度 $O(n^3)$ ,稍稍优化后可达到 $O(n^2)$
法三: $25\ pts$
观察 $5$ 到 $7$ 的测试数据可以发现权值的数据很小
那么我们就可以考虑枚举最大值,然后最小化模块个数 $m$
只需要在树上从根往下,不断删除超过最大值的节点即可
法四: $100\ pts$ (我好像就是这种解法???)
刚开始模拟时我们选择的是 $1$ 号节点,这是 $m$ 最小的方案,而我们是不断增大 $m$ 减少 $\max{w}$ 找到更优的方案
设我们选择了 $w_1, · · · ,w_m$ ,那么只有将最大的 $w_i$ ,替换成它的所有儿子,才能减少 $\max{w}$
所以我们可以用一个堆来维护目前已经选择的点,关键字为 $w_i$ ,每次选择最大的然后弹出,替换成它的儿子,同时更新答案。直到堆顶无法被分解时截止。
时间复杂度 $O(nlogn)$
T4 小学生计数题
题意
给定 $n$ 种难度以及每种难度的题数,问有多少种方案选择一些题目,使得它们的难度形成公差非 $0$ 的等差数列,且每个题目的难度都是公差的倍数
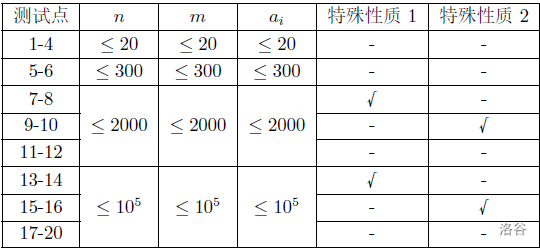
数据范围
对于所有测试点:
$1 \leq n, c_i \leq 10^5,0 \leq a_i \leq 10^5,m=\sum\limits_{i=1}^nc_i ≤ 10^5,2 ≤ L ≤ R ≤ m,a_i$
两两不同。
特殊性质 $1$ :满足 $R-L\leq10$
特殊性质 $2$ :满足所有 $c_i = 1$
思路
法一: $20\ pts$
直接二进制枚举可能的组题方式,然后检验长度是否在 $L$ 和 $R$ 之间以及是否为等差数列即可
时间复杂度 $O(n \times 2^n)$
法二: $30\ pts$
对于一种组题方式而言,如果确定了它的公差、首项、长度,那么这个题目集合就是唯一的
不妨暴力枚举这三个要素,同时在最内层从短到长枚举长度的过程中,不断乘上相应难度题目的数量进行统计
时间复杂度 $O(n^3)$
法三: $60\ pts$
调和级数枚举
先引入结论:(怎么证明呢?我也不知道,上网查资料吧)
考虑对上一档部分分的做法优化
在枚举完公差 $d$ 之后,可以考虑提取所有难度为 $d$ 的倍数的题目组成新的递增序列(后文为倍数序列)
不难发现一个合法答案就是倍数序列上的某一个长度合法的区间
然后我们只需要在倍数序列上再枚举长度和首项即可
时间复杂度:
对于公差 $d$ ,难度为 $d$ 的倍数的题目是不会超过$\frac{n}{d}$ 道的
$\therefore$ 时间复杂度为:
特殊性质 $1$ :$R-L\leq10$
我们可以对调和级数枚举的做法优化
先预处理出倍数序列的前缀和序列,在内层枚举长度的时候通过前缀积算出 $[1,L-1]$ 长度方案数的乘积,然后再去枚举 $[L,R]$ 的长度统计答案即可
时间复杂度约为 $O(n^2 logn \times ( R - L ))$
特殊性质 $2$ :$c_i = 1$
再对于调和级数枚举的做法进行优化
提取倍数序列后,因为 $c_i=1$ ,所以本质上只需要统计倍数序列中长度在 $[L,R]$ 之间的区间个数
那么就可以直接枚举右端点来统计有多少个合法的左端点即可
(当然可以推出来数学 $O(1)$ 公式,只是我不会)
设右端点的位置为 $x$ ,有 $cnt$ 个合法的左端点,那么有:
$x < L$ :$\quad$没有合法的左端点,即 $cnt=0$
$L \leq x \leq R$ :$\quad cnt=x-L+1$
$x > R$ : $cnt=R-L+1$
法四: $100\ pts$
结合所有的做法,我们可以考虑对于倍数序列 $f$ 预处理出前缀积 $g$ ,前缀积逆元的前缀和 $h$
那么枚举右端点 $x$ 时,可以计算出合法的方案数
这样对于每一个右端点即可 $O(1)$ 计算
时间复杂度(没有把逆元的时间复杂度算进去,可以 $O(n)$ 线性推 )为 $O(nlogn)$



